Numérique et sciences informatiques

Les algorithmes de tris

Le problème

Étant donné une liste de n nombres naturels, il faut la trier dans l'ordre croissant.

Il existe plusieurs algorithme de tris :

Le tri par insertion.

Le tri par sélection.

Le tri bulle.

Le tri à peigne.

Le tri Shaker.

Le tri Shell.

Le tri Gnome.

Le tri par tas.

Le tri fusion.

Le tri rapide.

...

On ne va pas tous les étudier...

Voici une simulation visuelle de quelques algorithmes de tris :

Tri visuelInformationsInformations[1]

SimulationLe tri par insertion 

Le programme ci-dessous vous permet de comprendre comment fonctionne un tri par insertion :

tri

Et pour ceux qui n'aurait pas encore compris :

Tri par insertion

Au début, on compare le 1er et le second en les échangeant si nécessaire

Puis on compare le 3ème avec le second (on les échange si c'est nécessaire ) et on compare avec le 1er ( on les échange si nécessaire)

Dès que l'échange n'est pas nécessaire on passe à l'étape suivante : ( le terme est alors à sa place)

On compare le 4ème avec le 3ème (etc...)

De manière plus globale :

Au bout d'un certain 'temps', on considère le kème élément.

Il faut le comparer à ses précédents ( en les échangeant si nécessaire ) et dès que cela n'est plus nécessaire on passe à l'élément suivant ( k+1)

Voici l'algorithme : avec deux boucles bornées

1
liste ( contient une liste de n nombres entiers aléatoirement choisis entre 0 et 100)
2
afficher la liste
3
4
pour k variant de 1 à n-1 ( n-1 car liste[n-1] est le dernier puisque liste[0] est le premier )
5
   pour j variant de k à 1 ( on décrémente de 1 )
6
     si liste[j-1]>liste[j] alors on les échange
7
8
afficher la liste (triée)
Ou bien celui-ci : avec une boucle bornée et une boucle non bornée.
On place un terme dans une variable temporaire (tmp).
On le compare avec ses précédents en les décalant d'un rang (à droite) s'ils lui sont supérieurs.
Dans celui-ci il n'y a pas d'échange, mais un simple déplacement de termes ( voir la première visualisation)
1
liste ( contient une liste de n nombres entiers aléatoirement choisis entre 0 et 100)
2
afficher la liste
3
4
pour k variant de 1 à n-1 ( n-1 car liste[n-1] est le dernier puisque liste[0] est le premier )
5
   tmp=liste[k]
6
   j=k
7
   tant que j>0  et  tmp<liste[j-1]
8
      on remplace liste[j] par liste[j-1]
9
      j=j-1
10
   liste[j]=tmp
11
12
afficher la liste (triée)
Vérifions la terminaison, la correction et la complétude de cet algorithme :
  • Pour le 1er algorithme : Les boucles étant bornées, la terminaison est assurée .
  • Pour le second : La boucle non bornée se termine car j est décrémenté de 1 tant qu'il est plus grand que 0.
Les algorithmes nous donnent bien une liste triée par ordre croissant...( des test nous le confirmerons, est-ce suffisant ?)
Dans ces algorithmes, pour une valeur de k, la partie de la liste à gauche de l'élément liste[k] est  triée.
  • Et tant que la liste contient des nombres comparables la complétude est assurée
Pour ce qui est du coût de cet algorithme :
En supposant le pire des cas ( où il faut effectuer des échanges (décalages) jusqu'au bout - le cas d'une liste déjà triée dans l'ordre décroissant)
En supposant également qu'un échange (décalage) vaut pour une opération...
  • pour k = 1 , on effectue 1 échange ( ou un décalage )
  • pour k=2, 2  échanges (ou 2 décalages)
  • pour k=3, 3 échanges (ou 3 décalages)
  • ....
  • pour k= n-1 , n-1 échanges (ou n-1 décalages)
Donc en tout : 
		
	
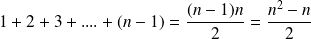
On dit dans ce cas que le coût est d'ordre 
		
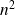	 ( ou quadratique )
Écrire les programmes correspondant en Python
Rajouter un compteur d'échanges...
ExempleCorrigé
Un programme possible :
1
# algorithme1
2
from random import*
3
liste=[]
4
compteur=0
5
for i in range(0,20,1):
6
    el=randint(0,100)
7
    liste.append(el)
8
print(liste)
9
print(len(liste))
10
L=len(liste)
11
12
for k in range(1,L,1):
13
    for j in range(k,0,-1):
14
        if liste[j-1]>liste[j]:
15
            temp=liste[j]
16
            liste[j]=liste[j-1]
17
            liste[j-1]=temp
18
            compteur=compteur+1
19
20
print(liste)
21
print("le nombre d'echange :" , compteur)
1
# algorithme2
2
from random import*
3
4
liste=[]
5
compteur=0
6
for i in range(0,20,1):
7
    el=randint(0,100)
8
    liste.append(el)
9
print(liste)
10
print(len(liste))
11
L=len(liste)
12
13
for k in range(1,L,1):
14
    tmp=liste[k]
15
    j=k
16
    while j>0 and tmp<liste[j-1]:
17
        liste[j]=liste[j-1]
18
        j=j-1
19
        compteur=compteur+1
20
    liste[j]=tmp
21
22
print(liste)
23
print("le nombre d'echange :" , compteur)
SimulationLe tri par sélection
En observant le tri par sélection ci-dessous :
  • Réalisez un algorithme de tri par sélection
  • Établir sa terminaison et sa complétude
  • Étudiez son coût


tri
Corrigé
Un programme possible
1
from random import *
2
liste=[]
3
compteur=0
4
for i in range(0,20,1):
5
    el=randint(0,100)
6
    liste.append(el)
7
print(liste)
8
print(len(liste))
9
L=len(liste)
10
compteur=0
11
for k in range(0,L-1,1):
12
    for j in range(k+1,L,1):
13
        if liste[j]<liste[k]:
14
            temp=liste[k]
15
            liste[k]=liste[j]
16
            liste[j]=temp
17
            compteur=compteur+1
18
print(liste)        
19
print("echange : ",compteur)
ComplémentPour les courageux
Réalisez un tri à bulle.
Un projet possible :
En vous inspirant du programme ci-dessous (Processing), comprendre et créer des visualisations de différents programmes de tris.
1
index=1
2
j=1
3
liste=[]
4
liste1=[]
5
couleur=[]
6
def setup():
7
    size(800,300)
8
    for i in range(0,30,1):
9
        el=int(random(1,100))
10
        liste.append(el)
11
        liste1.append(el)
12
    frameRate(10)
13
    textSize(12)
14
    for i in range(0,30,1):
15
        col=(int(random(0,256)),int(random(0,256)),int(random(0,256)))
16
        couleur.append(col)
17
        
18
        
19
def draw():
20
    background(0)
21
    for i in range(0,30,1):
22
        fill(255)
23
        text(liste1[i],25*i+30,50)
24
    for i in range(0,30,1):
25
        fill(255)
26
        text(liste[i],25*i+30,150)
27
        fill(couleur[i][0],couleur[i][1],couleur[i][2])
28
        rect(25*i+30,160,5,liste[i])
29
    tri_insertion()
30
31
        
32
def tri_insertion():
33
    global liste,j,index
34
    if j>0 and liste[j-1]>liste[j]:
35
        temp=liste[j]
36
        liste[j]=liste[j-1]
37
        liste[j-1]=temp
38
        temp2=couleur[j]
39
        couleur[j]=couleur[j-1]
40
        couleur[j-1]=temp2
41
        j=j-1
42
    else:
43
        index=index+1
44
        j=index
45
    if index==len(liste):
46
        noLoop()
47
        # visualisation    
48
    if index<len(liste):
49
        noFill()
50
        stroke(255, 0, 0)
51
        fill(255, 0, 0)
52
        ellipse(index*25+37, 145, 25, 25)
53
        noStroke()
54
        fill(255)
55
        text(liste[index], index*25+30, 150)
56
        noFill()
57
        stroke(0,255, 0)
58
        fill(0, 255, 0)
59
        ellipse(j*25+37, 145, 25, 25)
60
        fill(245,157,15)
61
        ellipse((j-1)*25+37,145,25,25)
62
        noStroke()
63
        fill(0,0,255)
64
        text(liste[j], j*25+30, 150)
65
        text(liste[j-1], (j-1)*25+30, 150)
  1. 
									Animation HTML5/JS réalisée par Nathan Gaberel, d'après l'applet Java réalisée par David Eck, adaptée en français par Tahia Benhaj-Abdellatif.
								
  2. La correction de l'algorithme
PrécédentPrécédentSuivantSuivant
AccueilAccueilImprimerImprimer
								Stéphan Van Zuijlen
								Licence de documentation libre GNURéalisé avec Scenari (nouvelle fenêtre)