Représentation de l'information.
Qu'entend-on par information ?
On peut dire que l'information est un ensemble de données ( écrits, images, sons, vidéos......) que l'on peut stocker,consulter, transformer ou transmettre à tout moment. Avant l'ère de l'informatique ( toute récente) la manière de conserver ces données dépendait du type des données.
|  |
Chacun sait aujourd'hui que toutes ces informations cohabitent dans un ordinateur sous forme de fichiers.
Un coup d'œil averti permet même de savoir quel type d'information contient tel ou tel fichier.
info.txt ou info.doc ou encore info.odt contiennent du texte.
info.jpg ou info.bmp ou encore info.png contiennent des images.
info.mp3 ou info. wav contiennent des sons.
info.avi ou info.divx contiennnent des vidéos.
Comment l'information peut-elle se représenter ?
L'idée fondamentale est que toute information a un reflet numérique.
Comme vous le savez sans doute , l'information est stockée sous forme d'une suite de 0 et de 1. Si on trouve une représentation numérique pour une information, par exemple la largeur d'une image, on pourra avec le système binaire l'écrire avec une suite de 0 et de 1. Il en va de même pour tout type d'information.
|  image 2 |
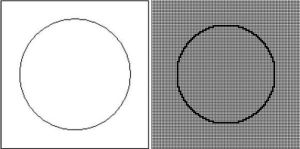
Fabriquer un reflet numérique d'un objet réel. Comment décrire ce dessin ? Une solution est de dire : « Cette image est formée d'un cercle ». Nous pouvons même être plus précis et indiquer les coordonnées du centre du cercle, son rayon, sa couleur, l'épaisseur du trait... À partir de cette description, n'importe qui pourrait reconstituer le dessin. |  cercle1 |
Cette méthode marche bien pour ce dessin-ci-dessus. Mais tout décrire avec des mots serait bien moins pratique pour le dessin suivant : En effet, comment facilement décrire en détail ces traits qui semblent tracés au hasard ? Qu'en serait-il avec un dessin représentant un objet réel, ou un visage ? |  image5 |
Une autre méthode, qui a l'avantage de pouvoir être utilisée pour n'importe quel dessin, consiste à superposer un quadrillage au tracé : Chacune des cases de ce quadrillage s'appelle un pixel (contraction de picture element, en anglais). On noircit ensuite les pixels qui contiennent une portion de trait : | 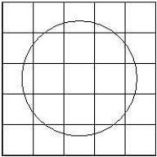 cercle2 |
 cercle3 | Puis, il nous suffit d'indiquer la couleur de chacun des pixels, en les lisant de gauche à droite et de haut en bas, comme un texte (dans notre culture occidentale). Ici, cela donne : blanc, noir, noir, noir, blanc, noir, noir, blanc, noir, noir, noir, blanc, blanc, blanc, noir, noir, noir , blanc, noir, noir, blanc, noir, noir, noir, blanc. De fait, cette description est assez approximative, et on constate une grande différence entre ces deux images : |
Mais nous pouvons rendre la description plus précise en utilisant un quadrillage, non plus de cinq x cinq, mais de cent x cent pixels : Et à partir de quelques millions de pixels, nous ne serions plus capables de faire la différence entre les deux images. Cette méthode est donc approximative, mais universelle : n'importe quel dessin, même très compliqué, se décrit exactement comme un dessin simple. Ce dessin se décrit donc par une suite de mots « blanc » ou « noir ». Comme seuls les mots « noir » ou « blanc » sont utilisés, nous pouvons être plus économes et remplacer chacun de ces mots par un seul symbole, par exemple le mot « noir » par la lettre « n » ou le chiffre « 0 » et le mot « blanc » par la lettre « b » ou le chiffre « 1 ». Le dessin ci-dessus, avec une grille de 5 x 5, se décrit alors par la suite de 25 chiffres : 1000100100011100010010001 Ces différentes descriptions sont équivalentes : le dessin se décrit toujours par une suite de symboles choisis parmi deux. Le nom de ces deux symboles importe peu, et nous pourrions les appeler noir et blanc ,a et b, 0 et 1, pile et face, - et +, Dupond et Dupont... que cela ne changerait pas grand-chose. On choisit 0 et 1. Ces symboles s'appellent les chiffres binaires ou bits (abréviation de binary digits, « chiffres binaires », en anglais). Une suite de 0 et de 1 s'appelle une suite binaire, ou parfois un mot binaire. Notre dessin se décrit ainsi avec 25 chiffres binaires, ou encore 25 bits ; sa longueur est 25. |
Bien entendu, il faut que nous soyons tous d'accord pour décrire tous les dessins de la même façon ! Comme nous l'avons fait dans l'exemple précédent, que le noir est représenté par 0 et le blanc par 1 et que les pixels se lisent de gauche à droite et de haut en bas.
Il faut se mettre d'accord sur un standard. Le codage de l'information est avant tout une affaire de... convention.
Regardons alors comment nous pourrions convenir de représenter d'autres objets.
Si nous voulons maintenant décrire une image en couleur, par exemple une image dans laquelle chaque pixel peut être noir, rouge, vert ou bleu, une première méthode consiste à la décrire par une suite dont chaque élément est l'un des quatre mots « noir », « rouge », « vert », « bleu ». Par exemple, prenons l'image suivante : Elle se décrit par la suite : noir, rouge, noir, rouge, noir, noir, rouge, noir, rouge, noir, bleu, noir, bleu, noir, vert, bleu, bleu , noir, bleu, vert, bleu, bleu, vert, vert, vert. Comme pour les images en noir et blanc, on peut être plus économe et décrire chaque couleur par une seule lettre ou un seul chiffre. Par exemple, en utilisant la correspondance
cette image se décrit par la suite : nrnrnnrnrnbnbnvbbnbvbbvvv Cette méthode utilise quatre symboles différents. Il est possible aussi de décrire cette image par une suite binaire, c'est-à-dire dans laquelle on utilise seulement deux symboles différents et non quatre. Mais comme il y a plus de deux couleurs, il est impossible de décrire chaque couleur par un seul chiffre binaire : un « 0 » ou « 1 ». En revanche, on peut décrire chaque couleur par une suite de deux bits. Par exemple :
|  image9 |
L'image ci-dessus se décrit alors par la suite
00 01 00 01 00 00 01 00 01 00 11 00 11 00 10 11 11 00 11 10 11 11 10 10 10
donc 25 x 2 = 50 bits. Les espaces entre chaque couple de valeurs binaires sont inutiles, sauf pour... en faciliter la lecture !
Une fois choisi le nombre de pixels de l'image (ici 5 x 5, pour une photo numérique il en faudrait quelques millions) et le nombre de bits sur lequel on représente la couleur de chaque pixel (ici 2 bits, en réalité de 8 à 32 bits, selon la palette des couleurs), toutes les images se représentent par une suite binaire de la même longueur : cette longueur s'obtient simplement en multipliant le nombre de pixels de l'image par le nombre de bits utilisés pour décrire la couleur d'un pixel. C'est ainsi que se décrivent les photographies dans les ordinateurs et les autres machines numériques.
Décrire des textes par des suites binaires
Décrire un texte semble à priori plus simple que décrire une image, puisqu'un texte est déjà une suite de symboles : c'est déjà une suite de lettres de l'alphabet. L'alphabet latin, que l'on utilise en français, contient 26 lettres. Mais en fait, quand on compte les majuscules et les minuscules, les lettres accentuées, les chiffres et les symboles de ponctuation, écrire en français nécessite plutôt une centaine de symboles.
Et puis, il faut aussi pouvoir décrire toutes les autres langues du monde.
Par exemple la phrase " tout se code en binaire" s'écrit en arabe " اى ان المدونة الثنائية ".
En utilisant le codage à 4 bits des 16 lettres ( inventé pour cette présentation) cela donne :
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
ء | آ | أ | ؤ | إ | ئ | ا | ث | د | ش | ف | ك | ل | ن | و | ي |
0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Cependant, là encore, pour partager les informations, il ne faut pas utiliser un code particulier comme celui-ci, mais un code standard, adopté par tous et qui représente tous les caractères de la langue utilisée. Les caractères les plus courants en Occident, ceux que nous tapons au clavier, sont codés sur 8 bits, avec un code universel, dit ASCII
(http://fr.wikipedia.org/wiki/American_Standard_Code_for_Information_Interchange) (pour American Standard Code for Information Interchange)
Pour coder tous les textes du monde, c'est l'Unicode, contenant plus de 120 000 caractères, qui est utilisé.
Ce standard utilise le code ASCII et des codes complémentaires à 16 ou 24 bits.
Comme toute information a un reflet numérique il nous reste à voir comment on code les nombres eux mêmes.