Codage des réels
Coder un nombre réel.
En informatique un réel est en fait un décimal....Nous sommes limités par le nombre de bits que nous réservons pour coder un nombre.
Considérons le nombre
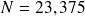, il est constitué d'une partie entière et d'une partie décimale.
En base 10 le nombre 23,375 se réécrit comme suit :
23,375 = 2x 10 +3 x 1 + 3 x 0,1 + 7 x 0,01 + 5 x 0,001...ce qui revient à écrire:
23,375 = 2 x 101 + 3 x 100 + 3 x 10-1 + 7 x 10-2 + 5 x 10-3
En base 2 le nombre 10111,011 se réécrit comme suit :
10111,011 = 1 x 24 + 0 x 23 + 1 x 22 + 1 x 21 + 1 x 20 + 0 x 2-1 + 1 x 2-2 + 1 x 2-3 ...soit:
10111,011 = 1 x 16 + 0 x 8 + 1 x 4 + 1 x 2 + 1 x 1 + 0 x 0,5 + 1 x 0,25 + 1 x 0,125
...c'est-à-dire 10111,0112 = 23,37510
Méthode : Écrire un décimal en binaire
On vient de voir que : 10111,0112 = 23,37510
Pour coder 23 en binaire c'est la méthode utilisée pour coder un nombre entier. 2310 =101112
Pour coder 0,375 on utilise la méthode suivante :
0,375 x 2 = 0,750 ....... ( ce qui signifie que : 0,375 = 0,750 x 2-1 =0 + 0,75 x 2-1).
O,750 x 2 = 1,5 ...........( ce qui signifie que : 0,75 = 1,5 x 2-1 soit encore que : ( 0,375 =( 1,5 x 2-1 ) x 2-1 = 1,5 x 2-2 = 1 x 2-2 + 0,5 x 2-2 ).
O,5 x 2 = 1 .................( ce qui signifie que : 0,5 = 1 x 2-1 soit encore que : ( 0,375 = 1 x 2-2 + ( 1 x 2-1 ) x 2-2 = 1 x 2-2 + 1 x 2-3 = 0,0112 ).
0n obtient ainsi : 23,37510 = 10111,0112 .
Cependant la virgule n'est pas codée.....
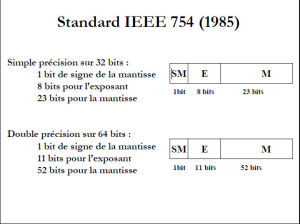
Le codage des réels avec le standard IEEE 754 ( 1985)
23,37510 = 10111,0112 = 1,0111011 x 24 ( simple manipulation arithmétique )
Le premier 1 est implicite et toujours présent pour n'importe quel nombre, on ne le codera pas...
On réservera un Bit pour le signe du nombre ( ici 0 car il est positif ).
En simple précision on réservera 8 bits pour l'exposant que l'on codera par " biais "
( la représentation biaisée, également appelée représentation par excès, consiste à considérer tout nombre binaire codé comme un entier non signé auquel on soustrait une constante définie selon le domaine de validité des entiers codés que l'on recherche. Ici cette constante est 127).
Et 23 bits pour la Mantisse ( la partie après la virgule)
 IEEE | Le standard IEEE 754 |
Méthode : Application à 23,375
23,37510 = 10111,0112 = 1,0111011 x 24
0 pour le signe.
L'exposant : Exposant - 127 = 4
Donc Exposant = 131 = 100000112 .
La mantisse 0111011.
D'où 23,37510 =
sur 32 bits
