Codage des nombres entiers
Décrire des nombres entiers
Le codage des valeurs numériques est de nature différente, car ce n'est pas un code arbitraire « standard », mais un choix issu de l'arithmétique.
En effet, il serait possible de représenter un nombre tel que 2741 comme la succession des caractères '2','7', '4' et '1', puis de coder chacun de ces caractères par son équivalent ASCII pour obtenir ainsi : 00110001 00110111 00110100 00110001. Mais, si un tel codage représente bien la chaîne de caractères '2741', il ne représente pas le nombre 2741 et ne permet pas d'effectuer dessus des calculs arithmétiques telle que l'addition ou la multiplication. Pour obtenir une représentation utilisable dans des calculs, il suffit cependant de passer de la numération à base 10 classique à la numération à base 2.
Découvrons ensemble le principe de ce changement de base.
Méthode : De la base 10 vers la base 2
L'écriture en base 10 de 2741 signifie que : 2741 = 2x103+7x102+4x101+1x100
Pour déterminer l'écriture de 2741 en base 2, il faut décomposer 2741 en puissance de 2.
2741=2x1370 + 1
1370 =2x685 + 0
685 = 2x342 + 1
342 = 2x171 + 0
171 = 2x85 + 1
85 = 2x42 + 1
42 = 2x21 +0
21 = 2x10 + 1
10 = 2x5 + 0
5= 2 x2+1
2=2x1 + 0
On obtient donc : [2741]10 =[ 101010110101]2
En effet :
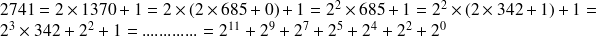
remarque : il faut au moins 12 bits pour coder ce nombre
Méthode : De la base 2 vers la base 10
Un nombre en base 2 : N=[ 101010110101]2
cela signifie que : N=
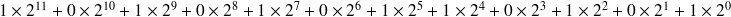=[2741]10
Complément : Codage des entiers sur 8 - 16 ou 32 bits
Si on dispose de 8 bits pour coder des entiers, le plus petit sera : 00000000 = 0 et le plus grand sera : 11111111=255. ce qui fait 256 nombres.(
).
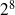remarque :
.
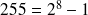Si maintenant on dispose de 16 bits ; on peut coder les nombres entiers de 0 à
.
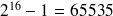Si maintenant on dispose de 32 bits ; on peut coder les nombres entiers de 0 à
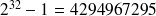. ( ce qui est déjà pas mal...)
Méthode : L'addition
 addition | L'addition en base 2 fonctionne comme l'addition que vous connaissez, sauf que ( 1 + 1 = 10, en fait 0 avec une retenue de 1). Exemple : prenons deux nombres : a = 21 = 00010101 et b = 25 = 00011001 codés sur 8 bits. En base 10 cela donne : a + b = 46 . En base deux cela donne : a + b = 00101110 ce qui fait bien 46. |
Méthode : La multiplication.
Reprenons nos deux nombres a et b .
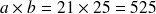
Or on ne peut pas obtenir 525 sur 8 bits, il faudra prévoir plus.....
 Multiplication | La méthode de multiplication est la même qu'en base 10 et attention aux retenues...( les lignes de 0 n'ont pas été écrites...) Il faudra au moins prévoir 16 bits pour stocker le résultat : 0000001000001101 |
Et les entiers négatifs ?
On pourrait coder des entiers "signés"en réservant un bit ( le 1er) pour signifier le signe.
par exemple +21= 00010101 et -21= 10010101. Cela a le désavantage de fabriquer deux zéros ( +0 et -0 ).
La méthode que nous retiendrons est celle dite du " complément à 2 "
Attention : Le complément à 2
Soit
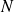un entier naturel codé en binaire sur 8 bits. On note
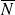le nombre tel que
.
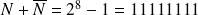Par exemple : 21 = 00010101 donne
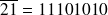
Un peu de mathématiques....
.
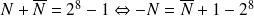Or
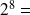100000000 qui sera interprété comme un zéro sur 8 bits car le 1 est sur le 9ème bit et ne sera pas pris en considération.
Ce qui nous amène à :
.
Et donc
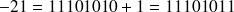
Ainsi
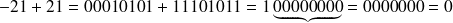sur 8 bits.
On retrouve un unique zéro et une méthode pour faire une soustraction.
Méthode : La soustraction.
Essayons la soustraction 25 - 21 = 4.
soit 25+ (-21)=00011001+11101011=
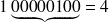sur 8 bits
Si on fait l'opération inverse : 21 -25 on trouve 11111100 = 252 qui correspond bien au complément à 2 de 4=00000100.
et le résultat est bien -4.
