Aller au contenu

Exercices⚓︎

Exercice 1

Écrire une fonction récursive puissance(x,n) qui calcule le nombre \(x^n\).

1
2
3
4
5
def puissance(x, n):
    if n == 0:
        return 1
    else:
        return x * puissance(x, n-1)

Exercice 2 ❤

On rappelle que le PGCD (plus grand diviseur commun de deux nombres) vérifie la propriété suivante : si la division euclidienne de \(a\) par \(b\) s'écrit \(a = b \times q + r\), alors \(pgcd(a,b)=pgcd(b,r)\).

Cette propriété est à la base de l'algorithme d'Euclide

Exemple : \(pgcd(24,18)=pgcd(18,6)=pgcd(6,0)\), donc \(pgcd(24,18)=6\)

Écrire un algorithme récursif pgcd(a,b).

1
2
3
4
5
def pgcd(a, b):
    if b == 0:
        return a
    else:
        return pgcd(b, a%b)

Exercice 3

La conjecture de Syracuse (ou de Collatz) postule ceci :

Prenons un nombre \(n\) : si \(n\) est pair, on le divise par 2, sinon on le multiplie par 3 puis on ajoute 1. On recommence cette opération tant que possible. Au bout d'un certain temps, on finira toujours par tomber sur le nombre 1.

  1. Proposer un programme récursif syracuse(n) écrivant tous les termes de la suite de Syracuse, s'arrêtant (on l'espère) à la valeur 1.
  2. On appelle «temps de vol» le nombre d'étapes nécessaires avant de retomber sur 1. Modifier la fonction précédente afin qu'elle affiche le temps de vol pour tout nombre n.

1. 

1
2
3
4
5
6
7
8
def syracuse(n):
    print(n)
    if n == 1:
        return None
    if n % 2 == 0:
        syracuse(n // 2)
    else:
        syracuse(3*n + 1)
2. 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
def syracuse(n, t=0):
    print(n)
    t += 1
    if n == 1:
        print('temps de vol :', t)
        return None
    if n % 2 == 0:
        syracuse(n // 2, t)
    else:
        syracuse(3*n + 1, t)

Exercice 4

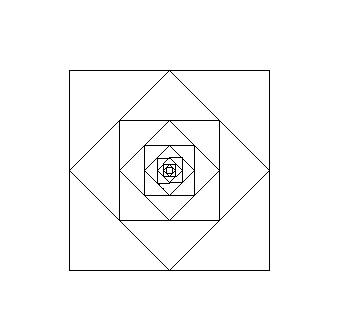
Reproduire le dessin suivant, à l'aide du module turtle.

turtle est un hommage au langage LOGO inventé par Seymour Papert au MIT à la fin des années 60.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
from turtle import *
def carre(c):
    for k in range(4):
        forward(c)
        right(90)

def base(c):
    carre(c)
    forward(c/2)
    right(45)

def trace(c, n):
    if n == 0 :
        return None
    else :
        base(c)
        c = c/(2**0.5)
        return trace(c, n-1)

trace(200, 5)

Exercice 5

Proposer une nouvelle fonction récursive puissance_mod(x,n) qui calcule le nombre \(x^n\). Pour optimiser la fonction déjà construite à l'exercice 1, utiliser le fait que :

  • si \(n\) est pair, \(a^n=(a \times a)^{n/2}\)
  • sinon \(a^n=a \times (a \times a)^{(n-1)/2}\)
1
2
3
4
5
6
7
8
def puissance_mod(x,n):
    if n == 0 :
        return 1
    else :
        if n % 2 == 0:
            return puissance_mod(x*x,n//2)
        else :
            return x*puissance_mod(x*x,(n-1)//2)

Exercice 6

Écrire un algorithme récursif recherche(lst,m) qui recherche la présence de la valeur m dans une liste triée (par ordre croissant) lst.

Cette fonction doit renvoyer un booléen.

Aide :

Les techniques de slicing (hors-programme) permettent de couper une liste en deux : 

>>> lst = [10, 12, 15, 17, 18, 20, 22]
>>> lst[:3]
[10, 12, 15]
>>> lst[3:]
[17, 18, 20, 22]


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
def recherche(lst,m):
    print(lst) # pour voir la taille de la liste diminuer
    if len(lst) == 1 :  #cas de base
        if lst[0] == m :
            return True
        else :
            return False
    else :              #cas récursif
        mid = len(lst)//2
        if lst[mid] > m :
            return recherche(lst[:mid],m)
        else :
            return recherche(lst[mid:],m)

Exercice 7

On considère le jeu des Tours de Hanoï. Le but est de faire passer toutes les assiettes de A vers C, sachant qu'une assiette ne peut être déposée que sur une assiette de diamètre inférieur.

Une version jouable en ligne peut être trouvée ici.

  1. S'entraîner et essayer d'établir une stratégie de victoire.
  2. Observer les images ci-dessous :

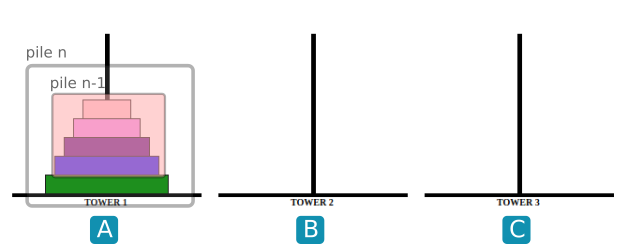
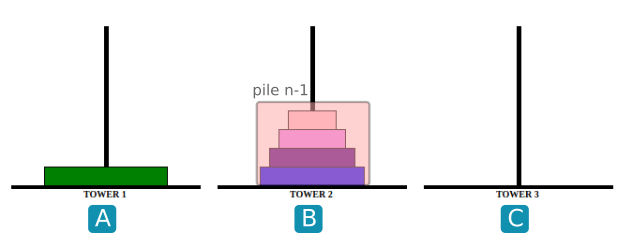
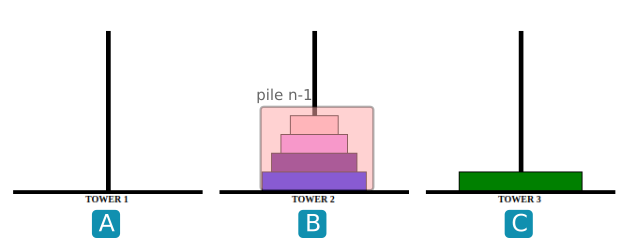
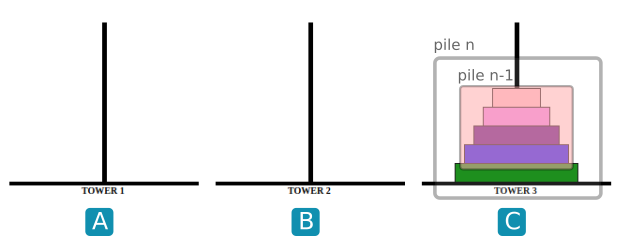
Écrire une fonction récursive hanoi(n, A, B, C) qui donnera la suite d'instructions (sous la forme " A vers C") pour faire passer une pile de taille n de A vers C en prenant B comme intermédiaire.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
def hanoi(n, depart, inter, arrivee):
    """ n : nombre d'assiettes dans la pile
    # depart : la pile de départ("A", "B" ou "C")
    # inter : la pile intermédaire("A", "B" ou "C")
    # arrivee : la pile d'arrivée ("A", "B" ou "C") """

    if n == 1 :
        print(depart + " vers " + arrivee)
    else :
        hanoi(n-1, depart, arrivee, inter) 
        print(depart + " vers " + arrivee)
        hanoi(n-1, inter, depart, arrivee)

hanoi(5, "A", "B", "C")

Exercice 8

Cet exercice a pour objectif le tracé du flocon de Von Koch.

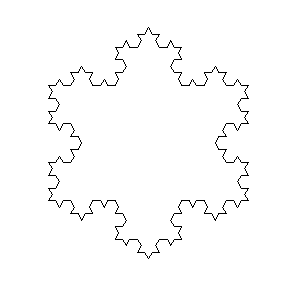
L'idée est de répéter de manière récursive la transformation ci-dessous : chaque segment de longueur l donne naissance à 4 segments de longueur l/3, en construisant une pointe de triangle équilatéral sur le deuxième tiers du segment.

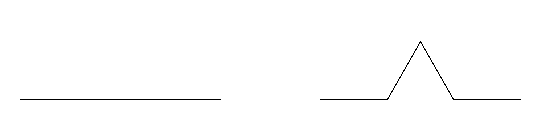
1) Créer une fonction récursive floc(n,l) qui trace à une «profondeur» n un segment de longueur l. 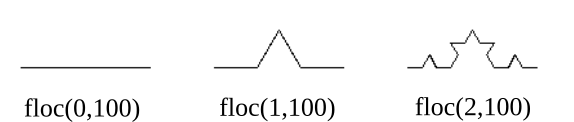Indications

  • l'instruction de tracé n'a lieu que quand n vaut 0.
  • l'étape n fait 4 appels sucessifs à l'étape n-1.

2) Créer une fonction triangle(n,l) qui trace le flocon complet.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from turtle import *

def floc(n, l):
    if n == 0:
        forward(l)
    else:
        floc(n-1,l/3)
        left(60)
        floc(n-1,l/3)
        right(120)
        floc(n-1,l/3)
        left(60)
        floc(n-1,l/3)


speed(0)

def triangle(n,l):
    for _ in range(3):
        floc(n,l)
        right(120)

triangle(5,400)

Exercice 9

Exercice de diffusion récursive sur Capytale à retrouver ici

image

Bibliographie
  • Numérique et Sciences Informatiques, Terminale, T. BALABONSKI, S. CONCHON, J.-C. FILLIATRE, K. NGUYEN, éditions ELLIPSES.
  • Prépabac NSI, Terminale, G.CONNAN, V.PETROV, G.ROZSAVOLGYI, L.SIGNAC, éditions HATIER.
Dernière mise à jour: 6 octobre 2022