Les bases de l'algorithmique
Un problème - Un algorithme
Considérons le problème suivant : Obtenir le plus grand d'une liste de n entiers naturels.
Pour construire un algorithme, nous devons utiliser un enchaînement d'opérations, qui manipulent :
Des données ( variables, constantes, tableaux, listes...)
Des structures de contrôles ( conditions, boucles..)
Le tout organisé de manière séquentielle : c'est à dire sous forme d'une suite d'instructions.
Un algorithme n'est pas un programme écrit dans un langage de programmation.
Pour l'exprimer on utilise notre langage naturel, et souvent un pseudo-langage, facilement transposable dans n'importe quel langage de programmation
Revenons à notre problème :
On dispose d'une liste de n entiers naturels :
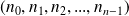
On recherche le plus grand d'entre eux.
La méthode la plus naturelle consiste à créer une variable max qui contient au départ
.
Puis de la comparer à chacun des
autres termes de la liste en la remplaçant par le terme comparé si celui-ci est plus grand.
Notre algorithme est écrit...
Ce n'est peut-être pas la meilleur façon de l'exprimer.
Faisons mieux, en faisant apparaître les données et les structures de contrôles que nous devons utiliser
maliste (contient une liste de n nombres entiers naturels)
max=maliste[0] (max contient le premier élément de cette liste)
pour i allant de 1 à n-1
si max<maliste[i] alors max=maliste[i] (on compare max et maliste[i])
afficher max
Les données utilisées sont : une liste et une variable
Les structures de contrôles sont : une boucle et une condition
Une fois l'algorithme écrit, il faut s'assurer de :
Sa terminaison : ( être certain que l'algorithme se termine)
Sa correction : ( être certain que le résultat est la (ou une) solution du problème)
Sa complétude : ( être certain que l'algorithme reste correct si (dans notre cas) on modifie la liste d'entiers naturels du départ)
Notre algorithme se termine bien puisqu'on effectue une boucle bornée ( pour... )
Il est correct puisqu'à chaque pas, max contient le plus grand
Et enfin, sa complétude est évidement assurée ( si la liste contient des nombres que l'on peut comparer..) .
On s'intéresse également aux nombres d'opérations que fait cet algorithme...
il y a : ( on ne considère pas l'affichage)
affectation : max=maliste[0]
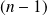comparaisons ( boucle )
Donc en tout :
opérations
On dit dans ce cas que le coût est d'ordre
( ou linéaire )
Simulation : Le programme
Vous devez traduire l'algorithme précédent en Python ( Processing ou EduPython ) sur une liste de 30 entiers naturels
Pour rappel : Remplir une liste de 30 nombres entiers compris entre 0 et 100 de manière aléatoire :
maliste=[]for i in range(0,30,1):
maliste.append(int(random(0,101)))
Exemple : Corrigé
Un code possible :
maliste=[]def compare(x,y):
if x>y:
return x
else:return y
for i in range(0,30,1):
maliste.append(int(random(0,101)))
max=maliste[0]
for i in range(1,30,1):
max=compare(max,maliste[i])
print(maliste)
print(max)
Simulation : Travail à réaliser
Reprendre l'ensemble en utilisant une boucle non bornée ( tant que... )
