Algorithme de dichotomie
Un algorithme de recherche d'un élément dans une liste triée.
La recherche d'un objet dans une liste ( dictionnaires, annuaires, moteur de recherche.....)
Le principe utilisé est la dichotomie .
Soit une liste de n objets classés. On recherche un objet en particulier.
--> On choisit dans la liste l'objet médian.
--> On compare les deux objets.
--> Si on a trouvé alors c'est fini.
--> Si l'objet recherché est placé avant l'objet choisi alors on recommence avec cette partie de la liste.
--> Si l'objet recherché est placé après l'objet choisi alors on recommence avec cette partie de la liste.
--> Au bout d'un certain nombre d'essais (cela se calcule) soit on a trouvé l'objet soit il n'est pas dans la liste.
Ce principe est utilisé aussi bien en mathématiques (pour rechercher une approximation de solution d'une équation) que pour trouver un mot dans un dictionnaire.
Voici cet algorithme sous forme d'une fonction.
On suppose que tab est un tableau de mots classés.
et que l'on recherche le mot contenu dans x.
Cette fonction renvoie un booléen.
Vrai si le mot est dans la liste
Faux s'il n'y est pas
tableau est une liste triée de longueur n
fonction recherche(tableau,x)
i=0 et j=n-1
tant que i<=j
si tableau[(i+j)//2]==x
retourner Vrai
sinon
si tableau[(i+j)//2]>x
j=(i+j)//2-1
sinon
i=(i+j)//2+1
retourner Faux
Il y a beaucoup d'autres algorithmes de recherche et la plupart d'entre eux sont des améliorations de celui-ci.
Ce qui compte c'est le temps d'exécution.
Imaginons un annuaire qui contienne les noms, prénoms, adresses.....des 7 milliards d'êtres humains vivant sur la terre.
Quel est le nombre maximum d'itérations pour trouver un individu ?
Comme à chaque itération on divise le nombre de personne par 2, et, en supposant que la personne cherchée est la 1ère ou la dernière. La question revient à :
Combien de fois faut-il que je divise 7 milliards par 2 pour qu'il n'en reste qu'un ?
Soit à résoudre l'équation :
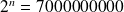dont la solution est :
. Soit au maximum 33 itérations !
Un algorithme qui balaye la liste du début à la fin aurait fait 1 itération pour la première personne et 7 milliards d'itérations pour la dernière ! !
Méthode : Exemple
Commençons par réaliser un programme de recherche par dichotomie d'un entier dans une liste triée qui compte le nombre de comparaison.
On travaillera avec EduPython.
Initialisation de la liste :
liste=[]for i in range(1,101,1):
liste.append(i)
La fonction recherche dichotomique :
Avec des paramètres
Un compteur ( qui compte le nombre de comparaisons)
Dont le résultat est un tuples (Vrai/Faux, compteur )
#fonction de recherche dichotomiquedef recherche(liste,x):
i=0
j=len(liste)-1
c=0 #compteur
while i<=j:
if liste[(i+j)//2]==x:
c=c+1
return (True,c)
else:if liste[(i+j)//2]>x:
j=(i+j)//2-1
c=c+1
else:i=(i+j)//2+1
c=c+1
return (False,c)
La recherche se fait sur l'entrée faite par l’utilisateur
# Demande d'entréex=int(input("Entrez un entier entre 1 et "+str(len(liste))))
#Appel de la fonction rechercheresultat=recherche(liste,x)
print(resultat)
Faites fonctionner ce programme en essayant différentes valeurs de x et différentes tailles de liste
Simulation : Un Jeu
Concevoir un programme qui illustre la situation suivante :
Stéphane (S) propose à Patrice (P) le jeu suivant :
"choisis en secret un nombre compris entre 0 et 100; je vais essayer de le deviner le plus rapidement possible, en ne pouvant que te poser des questions auxquelles tu réponds par oui ou par non ".
Deux cas sont envisageables :
Stéphane dans le rôle de l'ordinateur
Patrice dans le rôle de l'ordinateur
Méthode : Corrigés
Le cas où c'est l'ordinateur qui cherche :
# Créé par vstep, le 23/02/2019 en Python 3.4# c'est l'ordinateur qui cherche# x nombre à trouver pensé par l'utilisateurdef recherche(x):
k=True
a=0
b=100
c=0 #compteur
while k==True:
test=input("Le nombre est il égal à :" +str((a+b)//2)+" ?\n :Répondre par 'o' ou 'n'")
c=c+1
if test=='o':
return ((a+b)//2 ,c)
k=False
else:test=input("le nombre inconnu est-il plus grand que " + str((a+b)//2)+"?\n : Répondre par 'o' / 'n' ")
if test=="o":
a=(a+b)//2+1
else:b=(a+b)//2-1
resul=recherche(26)
print("le nombre cherché est " +str(resul[0])+" trouvé en "+str(resul[1])+" coups")
print(resul)
Le cas ou c'est l'utilisateur qui cherche
# Créé par vstep, le 23/02/2019 en Python 3.4# l'utilisateur est celui qui cherche# c'est l'utilisateur qui cherchefrom random import*
n=randint(0,100)
app=" "
var=input("Entrez un nombre")
var=int(var)
while True:
if var<n:
print(str(var)+ " : Trop bas")
var=input("Entrez un nombre")
var=int(var)
else:print(str(var)+ " : Trop haut")
var=input("Entrez un nombre")
var=int(var)
if var==n:
print("Bravo")
break
